量子力学中,可观测物理量的本征值为实数,对应的算符具有厄米性。二十年前,人们发现非厄米算符的本征值也可以为实数,但这类算符需要满足宇称和时间共同作用的对称性。当前,具有该对称性的非厄米量子力学已成为物理学研究的重要领域,随之涌现出大量实验平台揭示此量子力学的特点和在实际中的广泛应用。其中,由于具有非线性的光学系统,在实验中方便引入非厄米性和宇称时间的对称性,故在该领域表现出优越的性质。
最近,物理系张永平教授与北京应用物理与计算数学研究所陈竹研究员、北京大学吴飙教授、日本冲绳科学技术大学Thomas Busch教授和里斯本大学Vladimir Konotop教授,合作研究了光学系统中非线性、宇称时间对称性和空间周期性三者的相互竞争关系,发现只有在三者共存时,能谱相对于布里渊区中心和边界变得不对称;随着非线性的加强,能谱的不对称性表现为倾斜的“圈结构”,同时这些圈可以链接最低的两个布洛赫能带,使得能隙消失。以前的研究结论----能隙关闭意味着宇称时间的相变,但他们的研究表明,圈结构存在下,能隙的消失并不会产生宇称时间相变,即非线性对于宇称时间相有充分的保护作用。同时,他们进一步通过双模近似理论理解能谱的非对称性和圈结构的存在性,并根据等效势理论给出了非线性对宇称时间相变影响的物理图像。
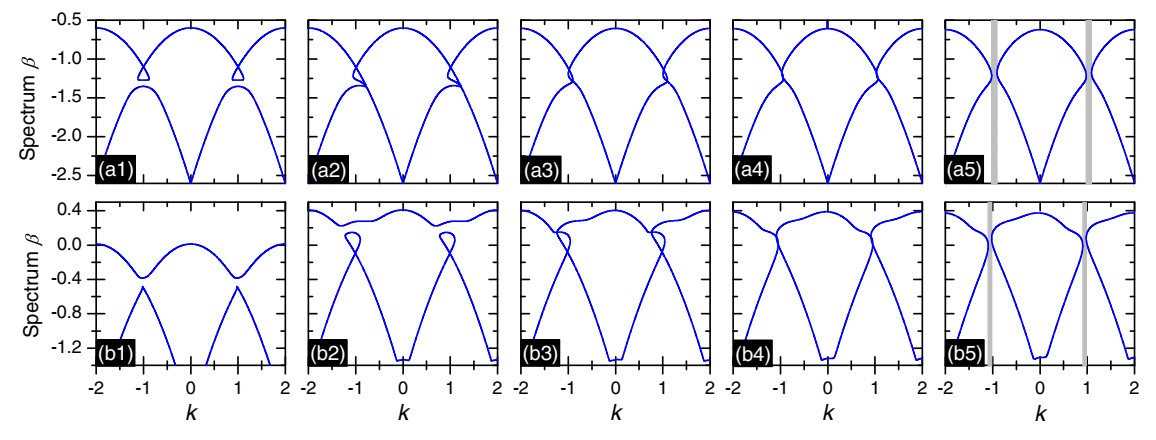
图示不同参数下非线性布洛赫能谱, 存在倾斜的“圈结构”。
这些圈能够链接两个能带,但不发生宇称时间相变
上述研究发表在近期的物理评论快报《Physical Review Letters》上。8455新葡萄场网站物理系张永平教授为论文的第一作者和共同通讯作者。该研究得到了国家自然科学基金面上项目(No.11974235和No.11774219)、国家重点研发计划、以及上海市量子信息技术科技重大专项支持。
论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.034101